WirelessBR

Esta página possui figuras grandes e fórmulas. Aguarde a carga se a conexão estiver lenta.

2.1.3    Difração em obstáculos

 Para a compreensão do mecanismo da difração em obstáculos, pode ser utilizado o Princípio de Huygens.

2.1.3.1.        Princípio de Huygens

 O Princípio de Huygens estabelece que cada ponto em uma frente de onda funciona como uma fonte de ondas secundárias (elementares), que comporão a frente de onda em uma nova posição ao longo da propagação. A Figura 3-6 ilustra o princípio.

Figura 3-6  -  Princípio de Huygens

Suponha-se agora que a frente de onda propagante encontre um obstáculo, como mostrado na Figura 3-7.

Figura 3-7  -  Obstrução da onda propagante por um obstáculo

 Uma porção da frente de onda será obstruída pelo obstáculo. Se analisarmos a propagação sem o princípio de Huygens, ou sem qualquer outra maneira de se considerar a difração, toda a região situada atrás do obstáculo não será iluminada (região de sombra). Porém, considerando a difração na análise, como feito através do princípio de Huygens, as fontes puntuais da região não obstruída emitirão frentes de onda secundárias que iluminarão a região situada atrás do obstáculo, como ilustra a Figura 3-7. Diz-se que a energia foi, então, difratada. Uma análise através da teoria eletromagnética mostra que a onda incidente induz correntes no obstáculo e que o campo irradiado por essas correntes constitui-se no campo difratado.

 Outro conceito importante no estudo da difração é o de Zonas de Fresnel e Elipsóides de Fresnel, apresentado diante.  

2.1.3.2.     Zonas e Elipsóides de Fresnel

 Analisando a Figura 3-8 ^[3], vemos que as frentes de onda oriundas de cada irradiador secundário percorrem distâncias distintas até alcançarem o ponto de observação O (pois estão distribuidas ao longo de toda a frente de onda). A análise da defasagem entre os campos associados aos diversos percursos gera o conceito das Zonas de Fresnel. A diferença de fase entre quaisquer dois percursos é dada por  , onde Dl é a

 diferença de comprimento entre os percursos considerados. Dessa forma, dependendo do caminho percorrido, cada fonte secundária dará uma contribuição positiva ou negativa ao campo recebido em O.

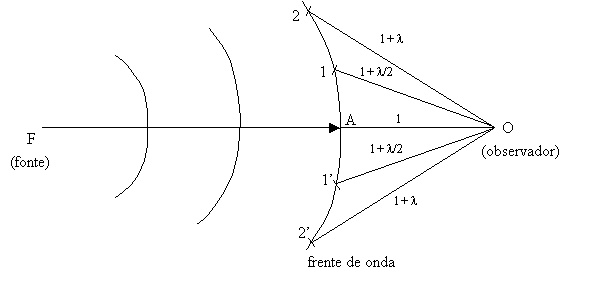
Figura 3-8  -  Distância entre pontos da frente de onda e um observador

 Se substituirmos a frente de onda da Figura 3-8 por um plano perpendicular ao percurso entre as antenas transmissora e receptora, pode-se fazer um cálculo aproximado da diferença de comprimento e, portanto, de fase, entre o percurso que une o ponto A (Figura 3-8) ao observador O (menor percurso entre um ponto na frente de onda e o ponto de observação) e qualquer outro percurso que chegue a O (oriundo de 1, 1’, 2 e 2’, por exemplo). Essa defasagem (em relação ao percurso perpendicular ao plano) é que será útil no conceito de Zonas de Fresnel. O procedimento de se considerar os percursos como sendo oriundos do plano, bem como os cálculos seguintes, são válidos quando se obedece, na geometria ilustrada na Figura 3-9 ^[1] a seguir, a  h << d₁ , d₂ , com (d₁ + d₂) denotando a distância entre transmissor e receptor.

   Figura 3-9  -  Geometria para cálculo de defasagem entre raios (determinação de Zonas de Fresnel)

 Na Figura 3-9, h é o raio de uma circunferência sobre o plano, centrada no ponto A. A diferença de comprimento entre um percurso que passa por A e um percurso que passa por qualquer outro ponto da circunferência de raio h é :

  ,  h << d₁ , d₂                                                                                         (3-32)

 A diferença de fase entre os percursos é dada por :

                                                                                    (3-33)

Denominando  é obtido :

                                                                                                (3-34) 

 O parâmetro n é chamado de parâmetro de difração de Fresnel-Kirchoff. ^[1]

 Delimitemos na Figura 3-8 uma porção da frente de onda centrada em A e que descreve um círculo (calota esférica) cujo diâmetro se estende do ponto 1 ao ponto 1’. Em toda essa região criada, os pontos da frente de onda distam de O de um valor entre l e l + l/2, ou seja, a máxima diferença de fase entre percursos que passam por essa região é dada por . Sejam os percursos que diferem do percurso que

 parte do ponto A de um valor máximo 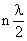, a região obtida corresponde a n = 1. A próxima região é o anel

 delimitado pelos pontos 1-1’ e 2-2’ e, da mesma forma, a máxima defasagem entre pontos situados no anel é de p radianos. Essa região corresponde a n = 2, pois a diferença de fase em relação ao percurso que se origina de A está situada entre p e 2p.

 As regiões assim formadas, com n a partir de 1, são denominadas Zonas de Fresnel. A primeira zona de Fresnel, por compreender variações de fase de zero a p radianos, gera contribuições que interferem construtivamente para o campo relativo ao percurso que começa em A. Pelos cálculos, observa-se que as zonas de Fresnel fornecerão, alternadamente, contribuições correspondentes a interferências construtivas e destrutivas para o campo total. É possível demonstrar que a área de cada zona é aproximadamente igual, de forma que as contribuições de campo no ponto O, vindas de cada duas zonas adjacentes, tenderiam a se anular. Porém, como as distâncias entre os pontos pertencentes a cada zona e o ponto de recepção O aumentam progressivamente com o aumento de n, as contribuições das zonas de maior ordem (n maior) tendem a ser menores (agora analisando a amplitude). Então, o que ocorre é que, a medida que se adiciona as contribuições das várias zonas de Fresnel, o campo resultante, inicialmente com oscilações de maior amplitude, tende a oscilar menos até chegar a um valor final. Ainda é interessante observar que, se fosse possível obstruir apenas as zonas de ordem par, ou seja, aquelas que geram contribuições correspondentes a interferências destrutivas para o campo da primeira zona de Fresnel (n = 1), o campo recebido seria maior que o de espaço livre, onde não há obstrução.

 Se agora considerarmos outras posições da frente de onda ao longo da propagação entre as antenas, conclui-se que, se forem unidos os limites de cada zona de Fresnel ao longo de toda a propagação, as figuras formadas serão elipsóides (com as antenas transmissora e receptora nos focos), denominados Elipsóides de Fresnel. A Figura 3-10 ilustra um elipsóide obtido para um valor de n qualquer. Da mesma forma que as zonas de Fresnel, é utilizada a denominação primeiro elipsóide de Fresnel, segundo elipsóide de Fresnel, e assim por diante, conforme o valor de n. Pela forma como são definidos, conclui-se que qualquer ponto situado na superfície de um elipsóide dista do ponto O de um valor que é  (n Î aos naturais positivos) 

 maior que o percurso oriundo de A. Assim, usando (3-32) :

                                                                                         (3-35)

A expressão (3-35) fornece o raio de um elipsóide de ordem n a uma distância d₁ da fonte, como ilustrado na Figura 3-10. 

  Figura 3-10  -  Elipsóide de Fresnel

2.1.3.3.       Difração por gume de faca

 Apresentados os conceitos importantes na compreensão da difração, a Figura 3-11 a seguir ilustra a geometria utilizada para a determinação do campo difratado por um obstáculo gume de faca (obstáculo de espessura infinitesimal e dimensão infinita na direção transversal à propagação, teoricamente). É importante observar que não é considerado o efeito da superfície da Terra na determinação da difração. 

Figura 3-11  -  Geometria da difração por gume de faca

 Alternativamente à expressão (3-32), a diferença de percurso D pode ser expressa por : ^[8]

  ,  h << d₁ , d₂                                                                                      (3-36)

onde :

a  -  como apresentado na Figura 3-11 [rad]

 E a diferença de fase fica :

                                                                                      (3-37)

 Lembrando que  e usando (3-37), o parâmetro n (expressões (3-33) e (3-34)) pode ser reescrito

 da seguinte forma : ^[2]

  ,  a < 0,2 radianos                                                                     (3-38)

 Para o entendimento da perda por difração, consideremos uma tela plana, perfeitamente absorvente, de dimensão transversal infinita, perpendicular ao percurso direto (linha de visada) entre transmissor e receptor. Enquanto a tela estiver a uma certa distância da linha de visada que une transmissor e receptor, seu efeito não será sentido no enlace. Na medida em que a tela é aproximada (movendo-se na vertical) da linha de visada, o campo recebido começará a oscilar, indicando obstrução sucessiva de zonas de Fresnel pares e ímpares. A Figura 3-12 ilustra um exemplo de campo difratado por um obstáculo gume de faca.

Figura 3-12  -  Campo difratado por obstáculo gume de faca

 Essa é a chamada difração por gume de faca e sua expressão exata (plotada na Figura 3-12) é obtida através das integrais de Fresnel. A expressão (3-39) a seguir é válida para a porção do gráfico de difração que apresenta queda monotônica com o parâmetro n : ^[2]

                                  (3-39)

 A expressão final de atenuação, incluindo a atenuação de espaço livre é, então :

         (3-40)

 Pela Figura 3-12, o ponto em que o campo vale E₀ (valor de campo no espaço livre) pela última vez ocorre para n @ -0,8. Esse ponto corresponde a uma liberação de 58 % do primeiro elipsóide de Fresnel em relação ao obstáculo e até aí considera-se que ainda não há obstrução. Quando a tela atinge a linha de visada, o campo tem seu valor reduzido à metade do valor em espaço livre, pois a porção inferior do elipsóide (ou superior, dependendo de onde vem a tela) foi inteiramente bloqueada.

 Se o obstáculo tem cume arredondado, há formulações empíricas para o cálculo da atenuação em excesso à atenuação de gume de faca, baseadas no raio do topo do obstáculo. Para o problema da difração por múltiplos obstáculos, há também desenvolvimentos empíricos.

 O cálculo da difração (simples ou múltipla) da forma como foi aqui exposto, é utilizado em enlaces ponto-a-ponto, onde identifica-se claramente um perfil (montanhoso, por exemplo) onde se possa aplicar as expressões. Não são metodologias de aplicação direta no cálculo de cobertura de sistemas celulares, uma vez que os métodos para previsão da perda de propagação em regiões urbanas já incluem, empiricamente, o efeito de obstrução por edificações. Entretanto, em casos no quais o relevo urbano é muito acidentado, é recomendável adicionar à perda prevista por estes métodos um termo correspondente a uma fração (40 a 50 % , tipicamente) da atenuação adicional por difração calculada da forma aqui descrita.

 A obtenção das três expressões de atenuação apresentadas (propagação em espaço livre, reflexão em Terra Plana e difração por gume de faca) baseou-se em uma descrição muito simplificada do cenário de propagação, permitindo que se chegasse às expressões com um bom grau de exatidão (considerando-se a descrição adotada para o cenário) e com relativa simplicidade. Numa situação real de propagação, a presença de construções e relevo de características aleatórias fará com que o ambiente seja muito diferente do descrito quando da obtenção das expressões (3-11), (3-24) e (3-40). A dificuldade no tratamento teórico de um ambiente complexo (especialmente grandes cidades e ambientes internos) levou ao surgimento de uma variedade de modelos empíricos e semi-empíricos para o cálculo de cobertura, discutidos em detalhe na Seção 3.4. 

2.2      Efeitos da atmosfera

 De uma forma geral, a atmosfera exerce uma influência importante na propagação de ondas de rádio. O efeito da chuva pode ser percebido para freqüências acima de 8 GHz, aproximadamente, causando atenuação, espalhamento e despolarização da onda propagante. Considerando-se a faixa de freqüências utilizada em comunicações móveis celulares, a chuva não apresenta problemas a esses sistemas.

 Outro efeito atmosférico importante, e que abrange todo o espectro de rádio-freqüências, é a refração atmosférica. Pressão atmosférica, temperatura e umidade variam com a altura, provocando variação no índice de refração atmosférica, dependente desses três parâmetros. As conseqüências da variação do índice de refração podem ser agrupadas em refração – encurvamento na trajetória dos raios, regido pela lei de Snell da refração; espalhamento – devido à formação de porções da atmosfera (“bolhas”) com índice de refração significativamente diferente do índice de refração das vizinhanças; e dutos – condição especial de comportamento do índice de refração, caracterizada pela inversão de seu gradiente entre certas alturas, fazendo com que a propagação da onda possa desviar-se da trajetória desejada (em sistemas ponto-a-ponto) sendo canalizada ao longo daquela região e podendo, inclusive, gerar interferência em sistemas distantes. Embora a refração seja gerada por uma variação uniforme do índice de refração, decrescente com o aumento da altura, e esteja sempre presente na atmosfera, os outros dois fenômenos constituem situações anômalas no comportamento do índice de refração.

 As condições anômalas são relevantes na propagação troposférica, afetando especialmente enlaces em microondas de algumas dezenas de quilômetros. Essas condições não são características da propagação terrestre (Figura 3-1). Porém, a variação temporal do índice de refração pode afetar também a propagação nos sistemas de comunicações móveis celulares. A dinâmica do índice de refração é um dos fatores que contribuem para o desvanecimento em larga escala do sinal, que será analisado adiante. Qualquer outra causa de atenuação devida à atmosfera (gases e neblina, por exemplo) não tem influência relevante nos sistemas celulares, ao menos para as faixas de freqüência atualmente utilizadas.