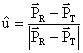WirelessBR

Esta página possui figuras grandes e fórmulas. Aguarde a carga se a conexão estiver lenta.

4.2.      Modelos Outdoor

 De maneira geral, os modelos empíricos para ambientes outdoor, usados na predição de propagação em microcélulas, podem ser expressos da seguinte forma :

 L = a + b logf + c logd’ + e logd   [dB]                                                                      (3-60)

onde:

a  -  constante [dB] determinada empiricamente ou a partir de modelos canônicos

b  -  fator de atenuação com a freqüência (relativo ao expoente de perda com a freqüência)

c  -  fator necessário quando o modelo utiliza uma distância de referência (d’ º d₀), e/ou quando o modelo utiliza mais de um valor para e (modelos de 2 slopes, onde, então, d’ º distância de ponto de quebra (d_bp)). Embora também haja modelos de mais de dois slopes, nenhum deles é aqui representado

e  -  fator de atenuação com a distância (relativo ao expoente de perda com a distância)

f  -  freqüência da portadora [MHz]

            d  -  distância entre transmissor (Tx) e receptor (Rx) [m]

d’  -  distância de referência (d₀) ou distância de ponto de quebra, conforme descrito na apresentação do fator c [m]

É feita a mesma subdivisão dos modelos quanto à faixa de freqüências já apresentada na descrição dos modelos indoor.

4.2.1.    Modelos para uma faixa larga de freqüências

 Excepcionalmente, nos dois modelos apresentados nesta Seção, a distância deverá estar em quilômetros.

4.2.1.1.                  COST-231 [7 ]

 O modelo proposto nessa referência apresenta como diferencial em relação à expressão (3-60) a sua dependência com a altura da estação base e do terminal móvel. Na expressão (3-60) :

a = 46,3 +C_M

onde :

            C_M = 0 , para cidades de tamanho médio é regiões suburbanas;

C_M = 3 , para metrópoles

b = 33,9

c = 0

e = 44,9 + 6,55 logh_b

onde :

h_b é a altura da estação base, em metros

f  -  o modelo foi desenvolvido para a faixa de 1500 a 2000 MHz

d  -  a faixa de validade do modelo é de 1 a 20 km. A distância deverá estar em km

 Há  no modelo duas parcelas adicionais, dependentes das alturas h_b (da base) e h_m (do móvel). São elas :

[-13,82 logh_b - a(h_m)]

onde a(h_m) é determinada pelas expressões apresentadas a seguir

 Para cidades pequenas e médias

a(h_m) = (1,1 logf - 0,7)h_m - (1,56 logf - 0,8)

 Para cidades grandes

a(h_m) = 3,2[log(11,75h_m)]² - 4,97     para f ³ 300 MHz

Observação

As faixas de valores de altura em que o modelo é válido são :

30 m £ h_b £ 200 m

1 m £ h_m £ 10 m

4.2.1.2.                  Modelo Walfish - Ikegami ^{[30], [2]}

 O modelo de Walfish - Ikegami apresenta uma expressão para as situações de visada direta (LOS) e um conjunto de expressões para os casos de obstrução (NLOS). A Figura 3-24 e a Figura 3-25 ilustram os parâmetros usados, especialmente para o modelo.

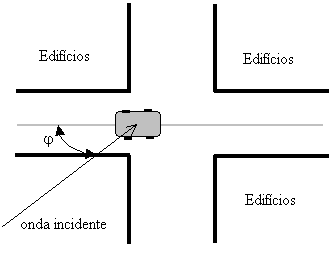
Figura 3-25  -  Modelo Walfish-Ikegami (vista superior da rua)

 Nas figuras :

            h_roof  -  altura média dos edifícios [m]

            h_móvel - altura da antena do móvel [m]

            W  -  largura média das ruas [m]

            b  -  separação média entre os edifícios [m]

            j  -  orientação da pista em relação ao enlace [graus]

 Modelo LOS

Na expressão (3-60) :

a = 42,6

b = 20

c = 0

e = 26

f  -  o modelo é válido na faixa de freqüências 800 MHz £ f £ 2 GHz

d  -  o modelo é válido para 20m £ d £ 5 km. A distância deverá estar em km

  Modelo NLOS

Por utilizar várias expressões, envolvendo os parâmetros descritos na Figura 3-24 e na Figura 3-25, a apresentação do modelo para NLOS não será feita através da forma padrão dada pela expressão (3-60). Assim como no modelo LOS, nas expressões que se seguem a freqüência é dada em MHz e a distância em km.

  L_NLOS = L₀ + L_rts + L_msd        para L_rts + L_msd ³ 0                                                        (3-61)

L_NLOS = L₀   ,                         para L_rts + L_msd < 0                                                       (3-62)

            onde :

                        L₀  -  atenuação de espaço livre, em dB

                        L_rts  -  atenuação devida a difração e espalhamento, em dB

                        L_msd  -  atenuação devida a difração múltipla, em dB

L₀ = 32,4 + 20logd + 20logf                                                               (3-63)

L_rts = -16,9 - 10logW + 10logf + 20logDh_móvel + L_ori                                   (3-64)

                                   se L_rts < 0  ®  L_rts = 0

Dh_móvel = h_roof - h_móvel                                                                                   (3-65)

Dh_base = h_base - h_roof                                                                                        (3-66)

L_ori = -10 + 0,354j                para 0 £ j £ 35^o                             (3-67)

L_ori = 2,5 + 0,075(j-35)        para 35^o £ j £ 55^o                         (3-68)

L_ori = 4 - 0,114(j-55)            para 55^o £ j £ 90^o                         (3-69)

L_msd = L_bsh + k_a + k_dlogd + k_flogf - 9logb                                            (3-70)

                                   se L_msd < 0  ®  L_msd = 0

L_bsh = -18log(1 + Dh_base)       para h_base > h_roof                                   (3-71)

L_bsh = 0                                  para h_base £ h_roof                                 (3-72)

k_a = 54                                   para h_base > h_roof                                (3-73)

k_a = 54 - 0,8Dh_base                para d ³ 0,5 km e h_base £ h_roof       (3-74)

k_a = 54 - 1,6Dh_base .d            para d < 0,5 km e h_base £ h_roof       (3-75)

k_d = 18                                   para h_base > h_roof                                (3-76)

                para h_base £ h_roof                                (3-77)

-        para cidades de tamanho médio e centros urbanos com densidade moderada de árvores :

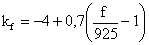                                                                    (3-78)

-        para centros metropolitanos

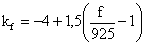                                                    (3-79)

k_a é um parâmetro que contabiliza o aumento da atenuação de propagação devido ao fato de as antenas de estações base estarem localizadas abaixo do topo dos edifícios adjacentes;

k_d e k_f determinam a dependência da difração múltipla com a freqüência.

Demais parâmetros presentes nas expressões são conforme já definidos nas figuras e na expressão (3-60).

Observação

A altura da base e do móvel é restrita aos seguintes limites :

4 m £ h_base £ 50 m

1 m £ h_móvel £ 3 m

4.2.2.    Modelos de freqüência única ou uma faixa estreita de freqüências

Nessa classe de modelos, assim como para modelos indoor, a freqüência não é um dado de entrada, de forma que b = 0 para todos os modelos.

4.2.2.1.                  Dual Slope [15], [7] e [6 ]

 As referências propõem um mesmo modelo, que subdivide a dependência da atenuação com a distância em duas faixas : uma anterior ao ponto de quebra d_bp e outra posterior a esse ponto. Esse é, portanto, um exemplo de modelo dual slope.

 Conforme Cheung et. al. [15], a expressão (3-60) fica :

Para as duas faixas de distância

f  -  o modelo foi obtido para a freqüência de 1,87 GHz

d  -  os parâmetros do modelo foram obtidos a partir de medições realizadas a distâncias de até 400 m

Para d₀ < d £ d_bp

a  -  atenuação obtida na distância de referência d₀ . Na ausência de valores medidos, o valor de a pode ser calculado pela expressão de atenuação em espaço livre.

c = -10n₁

e = 10n₁

d’  -  o modelo não faz referência ao valor utilizado (o valor usual é de 1 metro)

 Para d > d_bp

a  -  atenuação calculada em d = d_bp , usando a expressão (3-60) para o intervalo anterior (d₀ < d £ d_bp)

c = -10n₂

e = 10n₂

d’  -  é a própria distância d_bp

Observações

-        valores típicos para n₁ , n₂ e d_bp , citados em [15], para a freqüência de 1,87 GHz, são :

n₁ = 1,19

n₂ = 2,93

d_pq = 55 m

 -        a distância d_pq , onde se localiza o ponto de quebra, é dada por ^[7] :

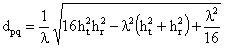                                                                         (3-80)

onde :

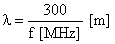  -  comprimento de onda                                                   (3-81)

h_b,m [m]  -  altura da base e do móvel, respectivamente

 Alternativamente, pode ser utilizada para o cálculo de d_pq a expressão (3-58), que se constitui numa aproximação para pequenos valores de comprimento de onda (alta freqüência).

Modelo das referências [7] e [6]

Em [6], Cátedra e Pérez-Arriaga propõem um modelo de mesmo formato do apresentado em [15]. O modelo sugere os seguintes valores, para a faixa de freqüências entre 1,8 e 1,9 GHz :

n₁  -  de 2 a 2,3

n₂  -  em torno de 3,3

 Além disso, o modelo de [6] menciona o uso da distância de referência d_0­ = 1 m.

 Em [7], Rappaport propõe um modelo com o mesmo formato do apresentado em [15] e também um modelo específico para situações de obstrução. O modelo de obstrução é exatamente o mesmo apresentado em [15] para distâncias d₀ < d £ d_pq , com a substituição de n₁ por um outro fator, n. O modelo de [7] utiliza a distância de referência d₀ = 1 m.

 Valores para n­₁ , n₂ e n (que substitui n₁ , em obstrução), para a freqüência de 1900 MHz, são apresentados na Tabela 3-6 ^[7].

Tabela 3-6 - Valores de coeficientes de atenuação com a distância, para 1900 MHz

Não é feita referência à faixa de distâncias de validade dos modelos apresentados em [7] e [6].

4.2.2.2.  Cátedra e Pérez-Arriaga [6]

Na referência [6] é também proposto um modelo decomposto para três regiões distintas de distância d. Na expressão (3-60) :

 Para as três decomposições do modelo

f  -  o modelo foi obtido para a freqüência de 2,2 GHz, aproximadamente

d  -  não é feita referência aos limites de distância de validade do modelo

 Para d < d_pq / 2

a = 40

c = 0

e = 25

 Para d_pq / 2 £ d < 4d_pq

a = 40 + 15log2

c = -15

e = 40

d’  -  é a própria distância d_pq

 Para d ³ 4d_pq

a = 40 - 25log2 - 20log4

c = 5

e = 60

d’  -  é a própria distância d_pq

Observação

Para o cálculo de d_pq é utilizada a expressão (3-80), ou a expressão (3-58).

O gráfico apresentado na Figura 3-26 é uma comparação entre modelos indoor apresentados nesta Seção. No gráfico, os modelos são identificados pelo número da Seção em que foram apresentados.

Figura 3-26  -  Comparação entre alguns dos modelos para ambientes indoor apresentados

(sem computar travessia de paredes ou andares)

 Quanto às curvas apresentadas na Figura 3-26, devem ser feitas duas observações. Os modelos 3.4.1.1.4  e  3.4.1.1.5 produzem o mesmo resultado se não há travessia de andares (FAF = 0  em  3.4.1.1.5), de forma que as curvas de ambos se superpõem na figura; e o modelo 3.4.1.2.1 está calculado para a freqüência de 1,9 GHz, para a qual é válido, ao contrário de todos os outros modelos, calculados para a freqüência de 914 MHz.

4.3.      Aplicação dos modelos

 A seguir são descritas metodologias para a implementação dos modelos (indoor e outdoor) descritos. Há duas categorias básicas, que diferem entre si na complexidade de implementação.

 1.      Modelos onde não é contabilizada explicitamente a travessia de obstáculos

-       deve ser criada uma malha de pontos de recepção. Na referência [24 ], por exemplo, é utilizado um espaçamento de 2 metros entre os pontos de recepção;

-       para cada ponto da malha de recepção criada, a atenuação L é calculada através da determinação da distância entre as antenas transmissora e receptora. Para isso, é utilizada a expressão de distância entre pontos apresentada no Apêndice 7.

2.      Modelos onde é computada explicitamente a travessia de obstáculos

-       assim como no item anterior, deve ser criada uma malha de recepção, bem como deve ser determinada a distância entre as antenas transmissora e receptora;

-       o passo adicional é determinar as interseções entre a linha que une as antenas transmissora e receptora e os obstáculos (paredes de forma geral e/ou pisos, dependendo do modelo). Para isso, é utilizado o procedimento de teste de sombreamento, descrito no Apêndice 4. Sendo P_T e P_R as coordenadas do transmissor (base) e do receptor (móvel), respectivamente, o vetor unitário do raio que une as antenas transmissora e receptora é dado por :

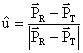                                                                                                 (3-82)

onde :

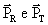  -  unem a origem do sistema de coordenadas cartesianas do cenário aos pontos P_R e P_T , respectivamente

Na metodologia descrita no Apêndice 4, as faces (obstáculos) deverão ter atributos indicando se a face é parede (e que tipo de parede, caso o modelo exija essa informação) ou piso, para que se multiplique o número de obstáculos de cada tipo pelo coeficiente adequado (atenuação unitária) na expressão de L. Alternativamente, a determinação de cruzamento de andares pode ser feita de uma forma mais simples, através de comparação entre as coordenadas dos pontos de Tx e Rx. Seja a Figura 3-27.

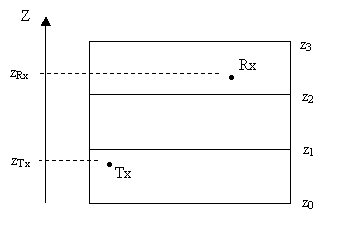
Figura 3-27  -  Exemplo de um edifício com três pisos, para aplicação dos modelos

No exemplo da Figura 3-27, conhecendo a componente z de Tx e Rx, é determinado o andar em que cada um está, através da identificação do intervalo ao qual a componente z pertence (se z está entre z₀ e z₁ , z₁ e z₂ ou entre z₂ e z₃). Uma vez feita a identificação para o Tx e o Rx,  a determinação do número de pisos entre eles é imediata.

Os modelos que não seguem exatamente essas duas metodologias, ou que não seguem apenas essas metodologias são :

-        modelo 3.4.1.2.1

Para o modelo de difração, a distância a ser determinada é entre o ponto “fonte virtual” e a antena receptora, e não entre as antenas transmissora e receptora;

-        modelo Walfish - Ikegami (3.4.2.1.2)

Além de seguir a metodologia 1, nesse modelo ainda é necessário obter o parâmetro j (inclinação do enlace, para cada ponto de recepção)

 O parâmetro j pode ser obtido da seguinte forma. Com o auxílio da Figura 3-25, sejam :

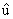 -  vetor unitário ao longo do raio incidente, dado pela expressão (3-82)

 -  vetor unitário na direção do percurso do móvel (vetor velocidade do móvel)

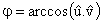                                                                                            (3-83)

A seguinte verificação deve ser aplicada para a correta determinação do ângulo j :

se j_calculado > p/2 então j = p - j_calculado

Este capítulo apresentou as características de rádio-propagação associadas aos sistemas celulares e, em conjunto com o Capítulo 2, que apresenta o conceito básico destes sistemas, provê o conteúdo essencial à compreensão dos fundamentos dos sistemas de comunicações móveis celulares (embora alguns conceitos envolvidos, especialmente neste capítulo, sejam de validade geral em sistemas rádio).

 O capítulo seguinte apresenta a teoria eletromagnética necessária ao cálculo de campos para a implementação de técnicas de traçado de raios, descritas em detalhes no Capítulo 5.

5.        Referências Bibliográficas

[1]  -  Notas de Aula do Curso de Canal de Propagação Rádio Móvel - Professor Glaucio Lima Siqueira, CETUC - PUC/Rio.

2]  -  Apostila e Notas de Aula do Curso de Propagação Troposférica - Professor Luiz Alencar Reis da Silva Mello, CETUC - PUC/Rio.

[3]  -  Gilberto Silva e O. Barradas, “Sistemas Radiovisibilidade”, vol. 1, 3^a edição, EMBRATEL.

[4]  -  Vijay K. Garg and Joseph E. Wilkes, “Wireless and Personal Communications Systems,” Prentice Hall, 1996.

[5]  -  John Gardiner and Barry West editors, “Personal Communication Systems and Technologies,” Artech House - Mobile Communications Series, 1995.

[6]  -  Manuel F. Cátedra and Jesús Pérez-Arriaga, “Cell Planning for Wireless Communications,” Artech House - Mobile Communications Series, 1999.

[7]  -  Theodore S. Rappaport, “Wireless Communications – Principles & Practice,” Prentice Hall Communications Engineering and Emerging Technologies Series, 1996.

[8]  -  J. D. Parsons, “The Mobile Radio Propagation Channel,” John Wiley & Sons, 1992.

[9]  -  Theodore S. Rappaport and Sandip Sandhu, “Radio-Wave Propagation for Emerging Wireless Personal-Communication Systems,” IEEE Ant. and Prop. Mag., vol. 36, no. 5, Out. 1994.

[10]  -  Rec. ITU-R P.1238, “Propagation Data and Prediction Models for the Planning of Indoor Radiocommunication Systems and Radio Local Area Networks in the Frequency Range 900 MHz to 100 GHz”.

[11]  -  Telesis Technologies Laboratory, Experimental License report to the FCC, Aug. 1991.  (citado em [9])

[12]  -  Henry L. Bertoni, Walter Honcharenko, Leandro Rocha Maciel and Howard H. Xia, “UHF Propagation Prediction for Wireless Personal Communications,” Proceedings of the IEEE, vol. 82, no. 9, Set. 1994.

[13]  -  H. H. Xia, H. L. Bertoni, L. R. Maciel, A. Lindsay-Stewart, and R. Rowe, “Radio propagation characteristics for line-of-sight microcellular and personal communications,” IEEE Trans. Ant. and Prop., vol. 41, no. 10, pp. 1439-1477, 1993. (citado em [12])

[14]  -  Howard H. Xia, Henry L. Bertoni, Leandro R. Maciel, Andrew Lindsay-Stewart and Robert Rowe, “Microcellular Propagation Characteristics for Personal Communications in Urban ans Suburban Environments,” IEEE Trans. on Veh. Technol., vol. 43, no. 3. Ago. 1994.

[15]  -  Joseph C. S. Cheung, Mark A. Beach and Shayne G. Chard, “Propagation measurements to support third generation mobile radio network planning,” 43^rd IEEE Vehicular Technology Conference, pp. 61-64, Meadowlands Hilton, Secaucus, New Jersey, USA, 18-20 de Maio, 1993.

[16]  -  E. H. Walker, “Penetration of Radio Signals Into Buildings in Cellular Radio Environment,” Bell System Technical Journal, 62, 9, 1983, pp. 2719-2735. (citado em [9])

[17]  -  A. M. D. Turkmani, J. D. Parsons, and D. G. Lewis, “Radio Propagation Into Buildings at 441, 900 and 1400 MHz,” Proceedings of the Fourth International Conference on Land Mobile Radio, Dez. 1987, pp. 129-138.

[18]  -  Kwok-Wai Cheung, Jonathan H.-M. Sau and R. D. Murch, “A New Empirical Model for Indoor Propagation Prediction,” IEEE Trans. on Veh. Technol., vol. 47, no. 3, Ago. 1998.

[19]  -  Walter Honcharenko, Henry L. Bertoni, James L. Dailing, J. Qian and H. D. Yee, “Mechanisms Governing UHF Propagation on Single Floors in Modern Office Buildings,” IEEE Trans. on Veh. Technol., vol. 41, no. 4, Nov. 1992.

[20]  -  W. Honcharenko, H. L. Bertoni and J. Dailing, “Mechanisms Governing Propagation Between Different Floors in Buildings,” IEEE Trans. on Ant. and Prop., vol. 41, no. 6, Jun. 1993.

[21]  -  Jean-François LaFortune and Michel Lecours, “Measurement and Modeling of Propagation Losses in a Building at 900 MHz,” IEEE Trans. on Veh. Technol., vol. 39, no. 2, Maio de 1990.

[22]  -  T. Okumura, E. Ohmori and K. Fukuda, “Field Strenght and Its Variability in VHF and UHF Land Mobile Services,” Review Electrical Communication Laboratory, vol. 16, no. 9-10, pp. 825-873, Set-Out 1968.

[23]  -  Masaharu Hata, “Empirical Formula for Propagation Loss in Land Mobile Radio Services,” IEEE Transactions on Vehicular Technology, vol. VT-29, no. 3, pp. 317-325, Ago. 1980.

[24]  -  G. K. Chan and F. A. Razaqpur, “Spectrum Requirements os an Indoor Pico-Cell Radio System,” IEEE Trans. Veh. Technol., vol. 44, no. 1, pp. 24-30, Fev. 1995.

[25]  -  Scott Y. Seidel and Theodore S. Rappaport, “914 MHz Path Loss Prediction Models for Indoor Wireless Communications in Multifloored Buildings,” IEEE Trans. on Ant. and Prop., vol. 40, no. 2, pp. 207-217, Fev. 1992.

[26]  -  F. C. Owen and C. D. Pudney, “Radio Propagation for Digital Cordless Telephones at 1700 MHz and 900 MHz,” Electronics Letters, 5 de Jan. 1989, vol. 25, no. 1.

[27]  -  Christer Törnevik, Jan-Erik Berg, Fredrik Lotse and Magnus Madfors, “Propagation Models, Cell Planning and Channel Allocation for Indoor Applications of Cellular Systems,” 43^rd IEEE Vehicular Technology Conference, Meadowlands Hilton, Secaucus, New Jersey, USA, 18-20 de Maio, 1993.

[28]  -  Purificación Bartolomé and Gema Vallejo, “Site Measurements for Installation of an Indoor Radio Communication System,” 43^rd IEEE Vehicular Technology Conference, Meadowlands Hilton, Secaucus, New Jersey, USA, 18-20 de Maio, 1993.

[29]  -  Asrar U. Sheikh, Martin Handforth and Majid Abdi, “Indoor Mobile Radio Channel at 946 MHz : Measurements and Modeling,” 43^rd IEEE Vehicular Technology Conference, Meadowlands Hilton, Secaucus, New Jersey, USA, 18-20 de Maio, 1993.

[30]  -  Leandro Rodrigues Coelho, “Cálculo de Cobertura e Planejamento de Sistemas CDMA”, Dissertação de Mestrado, Departamento de Engenharia Elétrica, PUC/Rio, Abril de 2000.